贝尔曼、动态规划、蒙特卡罗
《强化学习基础》
强化学习 (Reinforcement Learning)
下一篇:《强化学习基础》- 时序差分(TD)、SARSA、Q-learning
$\varepsilon$-greedy
\(a_{t}=\left\{\begin{array}{l}a_{t}^{*} \text { with probability } 1-\varepsilon \\ \text { random action with probability } \varepsilon\end{array}\right.\)
另一种表示法,二者意思一样:
\[\pi(a \mid s)=\left\{\begin{array}{ll} \varepsilon / m+1-\varepsilon & \text { if } a^{*}=\arg \max _{a \in A} Q(s, a) \\ \varepsilon / m & \text { else } \end{array}\right.\]强化学习8大要素
-
环境的状态S, t时刻环境的状态$S_t$是它的环境状态集中某一个状态。
-
个体的动作A, t时刻个体采取的动作$A_t$是它的动作集中某一个动作。
-
环境的奖励R, t时刻个体在状态St采取的动作$A_t$对应的奖励$R_{t+1}$会在t+1时刻得到。
-
个体的策略(policy) $\pi$, 它代表个体采取动作的依据,即个体会依据策略π来选择动作。最常见的策略表达方式是一个条件概率分布$\pi(a s)$, 即在状态s时采取动作a的概率。即$\pi(a s)=P(A_t=a S_t=s)$。概率大的动作被个体选择的概率较高。 -
个体在策略π和状态s时,采取行动后的价值(value),一般用$v_\pi(s)$表示。这个价值一般是一个期望函数。虽然当前动作会给一个延时奖励$R_{t+1}$,但是光看这个延时奖励是不行的,因为当前的延时奖励高,不代表到了t+1,t+2,…时刻的后续奖励也高。比如下象棋,我们可以某个动作可以吃掉对方的车,这个延时奖励是很高,但是接着后面我们输棋了。此时吃车的动作奖励值高但是价值并不高。因此我们的价值要综合考虑当前的延时奖励和后续的延时奖励。价值函数$v_\pi(s)$一般可以表示为下式,不同的算法会有对应的一些价值函数变种,但思路相同。: \(v_{\pi}(s)=\mathbb{E}_{\pi}\left(R_{t+1}+\gamma R_{t+2}+\gamma^{2} R_{t+3}+\ldots \mid S_{t}=s\right)\)
-
奖励衰减因子 $\gamma$,在[0,1]之间。如果为0,则是贪婪法,即价值只由当前延时奖励决定,如果是1,则所有的后续状态奖励和当前奖励一视同仁。大多数时候,我们会取一个0到1之间的数字,即当前延时奖励的权重比后续奖励的权重大。
-
环境的状态转化模型 $P^a_{ss′}$,可以理解为一个概率状态机,它可以表示为一个概率模型,即在状态s下采取动作a,转到下一个状态s′的概率。
- 探索率 $\varepsilon$,这个比率主要用在强化学习训练迭代过程中,由于我们一般会选择使当前轮迭代价值最大的动作,但是这会导致一些较好的但我们没有执行过的动作被错过。因此我们在训练选择最优动作时,会有一定的概率 $\varepsilon$ 不选择使当前轮迭代价值最大的动作,而选择其他的动作。
贝尔曼方程 (Bellman equation)
\(\begin{aligned} v_{\pi}(s) &=\mathbb{E}_{\pi}\left(R_{t+1}+\gamma R_{t+2}+\gamma^{2} R_{t+3}+\ldots \mid S_{t}=s\right) \\ &=\mathbb{E}_{\pi}\left(R_{t+1}+\gamma\left(R_{t+2}+\gamma R_{t+3}+\ldots\right) \mid S_{t}=s\right) \\ &=\mathbb{E}_{\pi}\left(R_{t+1}+\gamma G_{t+1} \mid S_{t}=s\right) \\ &=\mathbb{E}_{\pi}\left(R_{t+1}+\gamma v_{\pi}\left(S_{t+1}\right) \mid S_{t}=s\right) \end{aligned}\) 从上面方程可以看出,在 $t$ 时刻的状念 $S_{t}$ 和 $t+1$ 时亥的状交 $S_{t+1}$ 是满足递推关桃的,因此可以得出,
- 价值函数 $v_{\pi}(s)$ 的贝尔曼方程: \(v_{\pi}(s)=\mathbb{E}_{\pi}\left(R_{t+1}+\gamma v_{\pi}\left(S_{t+1}\right) \mid S_{t}=s\right)\)
- 动作价值函数 $q_{\pi}(s, a)$ 的贝尔曼方程: \(q_{\pi}(s, a)=\mathbb{E}_{\pi}\left(R_{t+1}+\gamma q_{\pi}\left(S_{t+1}, A_{t+1}\right) \mid S_{t}=s, A_{t}=a\right)\)
价值函数(state value fucntion) 与 动作价值函数(action-state value function)
从贝尔曼公式得到二者的计算公式:
价值函数: \(\begin{aligned} v_{\pi}(s)&=\sum_{a \in A} \pi(a \mid s) q_{\pi}(s, a) \\ &=\sum_{a \in A} \pi(a \mid s)\left(R_{s}^{a}+\gamma \sum_{s^{\prime} \in S} P_{s s^{\prime}}^{a} v_{\pi}\left(s^{\prime}\right)\right) \end{aligned}\)
动作价值函数: \(\begin{aligned} q_{\pi}(s, a)&=R_{s}^{a}+\gamma \sum_{s^{\prime} \in S} P_{s s^{\prime}}^{a} v_{\pi}\left(s^{\prime}\right)\\ &=R_{s}^{a}+\gamma \sum_{s^{\prime} \in S} P_{s s^{\prime}}^{a} \sum_{a^{\prime} \in A} \pi\left(a^{\prime} \mid s^{\prime}\right) q_{\pi}\left(s^{\prime}, a^{\prime}\right) \end{aligned}\)
最优价值函数: \(\begin{aligned} v_{*}(s) &=\max _{a} q_{*}(s, a) \\ &=\max _{a}\left(R_{s}^{a}+\gamma \sum_{s^{\prime} \in S} P_{s s^{\prime}}^{a} v_{*}\left(s^{\prime}\right)\right) \\ \end{aligned}\)
最优动作价值函数: \(\begin{aligned} q_{*}(s, a) &=R_{s}^{a}+\gamma \sum_{s^{\prime} \in S} P_{s s^{\prime}}^{a} v_{*}\left(s^{\prime}\right)\\ &=R_{s}^{a}+\gamma \sum_{s^{\prime} \in S} P_{s s^{\prime}}^{a} \max _{a^{\prime}} q_{*}\left(s^{\prime}, a^{\prime}\right) \end{aligned}\)
动态规划 (Dynamic programming)
强化学习的两个基本问题:
- 预测,即给定强化学习的6个要素,求解该策略的状态价值函数 $v(\pi)$:
- 状态集 $S$
- 动作集 $A$
- 模型状态转化概率矩阵 $P$
- 即时奖励 $R$
- 衰减因子 $\gamma$
- 给定策略 $\pi$
- 控制, 即给定强化学习的5个要素,求解最优的状态价值函数 $v_{}$ 和最优策略 $\pi_{}$:
- 状态集 $S$
- 动作集 $A$
- 模型状态转化概率矩阵 $P$
- 即时奖励 $R$
- 衰减因子 $\gamma$
求解预测问题
即策略评估 (Policy Evaluation),使用动态规划来求解强化学习的预测问题。
基本思路:从任意一个状态价值函数开始,依据给定的策略,结合贝尔曼期望方程、状态转移概率和奖励同步迭代更新状态价值函数,直至其收敛,得到该策略下最终的状态价值函数。
假设我们在第 $k$ 轮迭代已经计算出了所有的状态的状态价值, 那么在第 $k+1$ 轮我们可以利用第 $k$ 轮计算出的状态价值计算出第 $k+1$ 轮的状态价值。这是通过贝尔曼方程来完成的,即: \(v_{k+1}(s)=\sum_{a \in A} \pi(a \mid s)\left(R_{s}^{a}+\gamma \sum_{s^{\prime} \in S} P_{s s^{\prime}}^{a} v_{k}\left(s^{\prime}\right)\right)\)
求解控制问题
-
策略迭代(Policy Iteration)

-
价值迭代(Value Iteration)
- 和策略迭代相比,我们没有等到状态价值收敛才调整策略,而是随着状态价值的迭代及时调整策略, 这样可以大大减少迭代次数。此时我们的状态价值的更新方法也和策略迭代不同。现在的贝尔曼方程迭代式子如下: \(v_{k+1}(s)=\max _{a \in A}\left(R_{s}^{a}+\gamma \sum_{s^{\prime} \in S} P_{s s^{\prime}}^{a} v_{k}\left(s^{\prime}\right)\right)\)
- 算法伪代码:
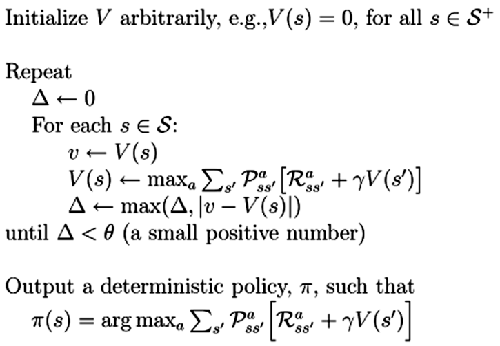
蒙特卡罗法 (Monte Carlo)
由于动态规划法需要在每一次回溯更新某一个状态的价值时,回溯到该状态的所有可能的后续状态。导致对于复杂问题计算量很大。同时很多时候,我们连环境的状态转化模型P都无法知道,这时动态规划法根本没法使用。
蒙特卡罗法是一种不基于模型(即概率转换模型 $P$)的强化学习方法。
问题定义 (少了 $P$ )
- 预测,即给定强化学习的5个要素,求解该策略的状态价值函数 $v(\pi)$:
- 状态集 $S$
- 动作集 $A$
- 即时奖励 $R$
- 衰减因子 $\gamma$
- 给定策略 $\pi$
- 控制, 即给定强化学习的5个要素,求解最优的状态价值函数 $v_{}$ 和最优策略 $\pi_{}$:
- 状态集 $S$
- 动作集 $A$
- 即时奖励 $R$
- 衰减因子 $\gamma$
- 探索率 $\varepsilon$
蒙特卡罗法通过采样若干经历完整的状态序列(episode)来估计状态的真实价值。所谓的经历完整,就是这个序列必须是达到终点的。 比如下棋问题分出输赢,驾车问题成功到达终点或者失败。有了很多组这样经历完整的状态序列,我们就可以来近似的估计状态价值,进而求解预测和控制问题了。
从特卡罗法法的特点来说,一是和动态规划比,它不需要依赖于模型状态转化概率。二是它从经历过的完整序列学习,完整的经历越多,学习效果越好。
求解预测问题/策略评估
-
给定策略 $\pi$ 的完整有T个状态的状态序列如下: $S_{1}, A_{1}, R_{2}, S_{2}, A_{2}, \ldots S_{t}, A_{t}, R_{t+1}, \ldots R_{T}, S_{T}$
-
再写一遍上面提到的状态价值函数:$v_{\pi}(s)=\mathbb{E}{\pi}\left(G{t} \mid S_{t}=s\right)=\mathbb{E}{\pi}\left(R{t+1}+\gamma R_{t+2}+\gamma^{2} R_{t+3}+\ldots \mid S_{t}=s\right)$
- 对于蒙特卡罗法来说,如果要求某一个状态的状态价值,只需要求出所有的完整序列中该状态出现时候的收获再取平均值即可近似求解,也就是:
\(\begin{gathered}
G_{t}=R_{t+1}+\gamma R_{t+2}+\gamma^{2} R_{t+3}+\ldots \gamma^{T-t-1} R_{T} \\
v_{\pi}(s) \approx \text { average }\left(G_{t}\right), s . t . S_{t}=s
\end{gathered}\)
注意:这里的$G_t$是长期回报,称为收获(Return),而$R_t$指的是在某个状态下采取动作得到的奖励,称为奖励(Reward)
- 优化:
- 同样一个状态可能在一个完整的状态序列中重复出现,此时计算return有两种方式: 1. 首次访问(first visit)蒙特卡罗法。仅把状态序列中第一次出现该状态时的收获值纳入到收获平均值的计算中; 2. 每次访问(every visit)蒙特卡罗法。针对一个状态序列中每次出现的该状态,都计算对应的收获值并纳入到收获平均值的计算中
- 累进更新平均值(incremental mean)。上面的average的公式意味着要保存所有该状态的收获值之和最后取平均。这样浪费了太多的存储空间。一个较好的方法是在迭代计算收获均值,即每次保存上一轮迭代得到的收获均值与次数,当计算得到当前轮的收获时,即可计算当前轮收获均值和次数。通过下面的公式就很容易理解这个过程: \(\mu_{k}=\frac{1}{k} \sum_{j=1}^{k} x_{j}=\frac{1}{k}\left(x_{k}+\sum_{j=1}^{k-1} x_{j}\right)=\frac{1}{k}\left(x_{k}+(k-1) \mu_{k-1}\right)=\mu_{k-1}+\frac{1}{k}\left(x_{k}-\mu_{k-1}\right)\) 这样上面的状态价值公式就可以改写成: \(\begin{gathered} N\left(S_{t}\right)=N\left(S_{t}\right)+1 \\ V\left(S_{t}\right)=V\left(S_{t}\right)+\frac{1}{N\left(S_{t}\right)}\left(G_{t}-V\left(S_{t}\right)\right) \end{gathered}\) 这样我们无论数据量是多还是少, 算法需要的内存基本是固定的。有时候, 尤其是海量数据做分布式迭代的时候, 我们可能无法准确计算当前的次数 $N\left(S_{t}\right)$, 这时我们可以用一个系数 $\alpha$ 来代替, 即: \(V\left(S_{t}\right)=V\left(S_{t}\right)+\alpha\left(G_{t}-V\left(S_{t}\right)\right)\) 对于动作价值函数 $Q\left(S_{t}, A_{t}\right)$, 也是类似的, 比如对上面最后一个式子,动作价值函数版本为: \(Q\left(S_{t}, A_{t}\right)=Q\left(S_{t}, A_{t}\right)+\alpha\left(G_{t}-Q\left(S_{t}, A_{t}\right)\right)\)
求解控制问题
与动态规划中 value iteration 思路类似, 每轮迭代先做策略评估,计算出价值$v_k(s)$,然后基于据一定的方法(比如贪婪法)更新当前策略$\pi$,最后得到最优价值函敘 $v_{}$ 和最优策略 $\pi_{ \circ}$
不同之处:
- 一般是优化最优动作价值函数$q_∗$,而不是状态价值函数$v_∗$
- 动态规划一般基于贪婪法更新策略。而蒙特卡罗法一般采用$\varepsilon$−贪婪法更新。即: 使用 $1-\varepsilon$ 的概率贪婪地选择目前认为是最大行为价值的行为,而用$\varepsilon$ 的概率随机的从所有m 个可选行为中选择。 \(\pi(a \mid s)=\left\{\begin{array}{ll} \varepsilon / m+1-\varepsilon & \text { if } a^{*}=\arg \max _{a \in A} Q(s, a) \\ \varepsilon / m & \text { else } \end{array}\right.\)
MC在线控制-算法伪代码:

蒙特卡罗优缺点总结:
- 优点:不需要环境模型(状态间概率转换模型)
- 缺点:需要任务能够结束才能得到return
下一篇:《强化学习基础》- 时序差分(TD)、SARSA、Q-learning
© 2022 weixians.github.io